农场悟道

Gradient Boosting 原理介绍

2018/03/04 机器学习 集成学习

集成学习通过构建并结合多个学习器来完成学习任务。通过将多个学习器进行结合，常可获得比单一学习器显著优越的泛化性能。集成学习的一般做法：先产生一组“个体学习器”，再用某种策略将它们结合起来。常见的集成策略有：Bagging、Boosting和Stacking。本文介绍Boosting的代表算法Gradient Boosting。

Boosting算法的主要思路：依次生成一个基学习器。每次迭代，忽略先前已生成的基学习器已经处理得很好的样本，重视之前的基学习器难以学习的样本，训练得到下一个基学习器。进行多次迭代，直到基学习器数目达到事先指定的值T，最后将T个基学习器进行加权结合。

Boosting的代表算法有：Adaboost和Gradient Boosting。Adaboost在每次迭代时，更新每个训练样本的权重，对难以正确分类的样本施加更多的权重，对已经分类正确的样本，减少其权重。新的基学习器基于更新权重的训练样本进行训练学习，使得新的基学习器更重视难以正确分类的样本。Gradient Boosting则将Boosting看作是一个数值优化问题，通过类似于梯度下降的步骤，依次地添加基学习器，以最小化损失函数为目标，在函数空间（假设集）里寻找一个最优函数。

1、算法原理

1.1 梯度下降

梯度下降是机器学习用于求解模型参数的常用方法。对于这样的典型优化问题：find $\hat{x}=\operatorname*{arg\,max}_x f(x)$，通常采用梯度下降求解，算法流程如下：

  • 给定一个起始点

  • 对于 $i=1,2,\dotsc,K$ 分别做如下迭代：

    (a) $x_i=x_{i-1}+\gamma_{i-1}* g_{i-1}$，这里的$g_{i-1}=-\left.\frac{\partial f}{\partial x}\right\vert_{x=x_{i-1}}$ 表示 $f$ 在 $x_{i-1}$ 点的梯度

  • 直到 $\vert g_{i-1}\vert$ 足够小，或者 $\vert x_i - x_{i-1}\vert$ 足够小，或者迭代次数达到指定值 $T$

在参数空间里寻找最优参数，以实现最小化目标函数的目标。整个寻优过程就是小步快跑的过程，每次都往目标函数下降最快的那个方向前进一小步。最后，得到的最优参数表示为加和形式：

1.2 Gradient Boosting

Gradient Boosting 由梯度下降启发而来。梯度下降是在参数空间里寻找一个最优点，Gradient Boosting可以理解为在函数空间（假设集）寻找一个最优函数。优化的目标通常是通过一个损失函数来定义：

常见的损失函数如平方差函数：$\text{Loss}(F(x_i),y_i)=(F(x_i)-y_i)^2$

我们采用类似梯度下降的方法，进行多次迭代，通过求取梯度的方式，依次构造基学习$f_1,f_2,f_3,\dotsc,f_m$ 。

最后得到的函数的形式为：

每次求取梯度时，我们对损失函数 $L$，以 $F$ 为参考求取梯度：$g_i=-\left.\frac{\partial L}{\partial F}\right\vert_{F=F_{i-1}}$ 。这里的 $F_{i-1}$ 是截至前一次迭代，求得的F函数。

一个函数对函数的求导不好理解，通常无法通过上述的公式直接求解到梯度函数 $g_i$ 。但是，对于每个训练样本，我们可以得到梯度 $g_i$ 在该训练样本上的值：

严格来说 $\hat{g_i}(x_k)\text{ for }k=1,2,\dotsb,N$ 只是描述了 $g_i$ 在某些个别点上的值，并不足以表达 $g_i$ ，但是但是我们可以通过函数拟合的方法从 $\hat{g_i}(x_k)\text{ for }k=1,2,\dotsb,N$ 构造 $g_i$ ，这样我们就通过近似的方法得到了函数对函数的梯度求导。若采用决策树来拟合（梯度提升与决策树相结合），即为当前业界流行的GBDT模型。

依次，Gradient Boosting 算法的过程可以总结如下：

  • 选择一个其实常量函数 $f_0$ 。常量函数 $f_0$ 通常取训练样本目标值的均值，即 $f_0=\frac{1}{N}\sideset{}{_{i=0}^N}\sum y_i$

  • 对于 $i=1,2,\dotsc,K$ 分别做如下迭代：

    (a) 计算离散梯度值 $\hat{g_i}(x_j)=-\left.\frac{\partial L}{\partial F(x_j)}\right\vert_{F=F_{i-1}}\text{for }j= 1,2,3,\dotsc,N$

    (b) 对 $\hat{g_i}\text{ for }j= 1,2,3,\dotsc,N$ 做函数拟合，得到 $g_{i-1}$

    (c) 通过 line search 得到 $\gamma_i=\operatorname*{arg\,min}L(F_{i-1}+\gamma_i * g_i)$

    (d) 令 $F_i=F_{i-1}+\gamma_i * g_i$

  • 直到 $\vert\hat{g_i}\vert$ 足够小，或者达到指定的迭代次数

具体的算法流程：

gbm

1.3 损失函数

Gradient Boosting 的损失函数必须是可微的。Gradient boosting 可适用于任意的可微的损失函数，其不但可用于二分类问题，还可用于回归问题、多类别分类问题。损失函数的选择视要解决的问题而定。

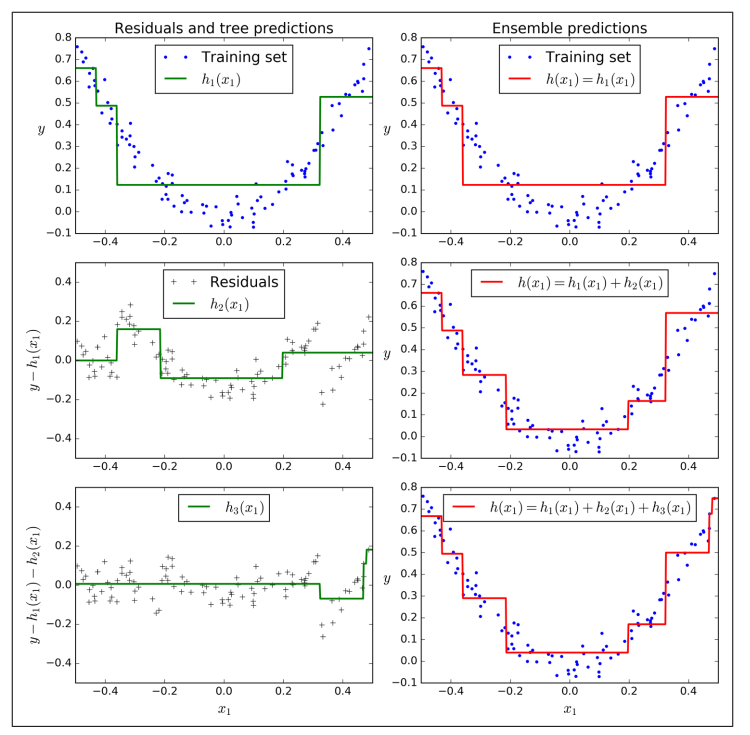
谈到流行的GBDT算法，常常听到一种简单的描述：“根据已有模型的预测值与样本的实际输出的残差，再构造一颗树。依次迭代，生成一系列的决策树“。其中这个说法不全面。它只是 Gradient Boosting 的一种特殊情况。这个说法仅适用于损失函数为平方差的情况。

每次迭代，基学习器拟合的目标值为 $\hat{g_i}(x_k)=-\left.\frac{\partial L}{\partial F(x_k)}\right\vert_{F=F_{i-1}}\text{for }k= 1,2,3,\dotsc,N$ ，以平方差损失函数为例，梯度为：

忽略倍数2，这正好是当前已构造的函数 $F_{i-1}$ 在样本上和目标值 $y_k$ 之间的差值。因此，当损失函数为平方差函数时，每次迭代会根据当前残差来生成一个基学习器。

fit_residuals

若以绝对差值 $\vert F(x_i)-y_i\vert$ 为损失函数，则梯度为符号函数：

平方差函数和绝对差值函数常用于回归类问题，平方差函数容易受到异常样本的影响，而绝对差值则对异常样本的健壮性更强。常见用于 Gradient Boosting 的损失函数还有：Huber Loss、KL-divergence、logloss 等。

2、GBDT

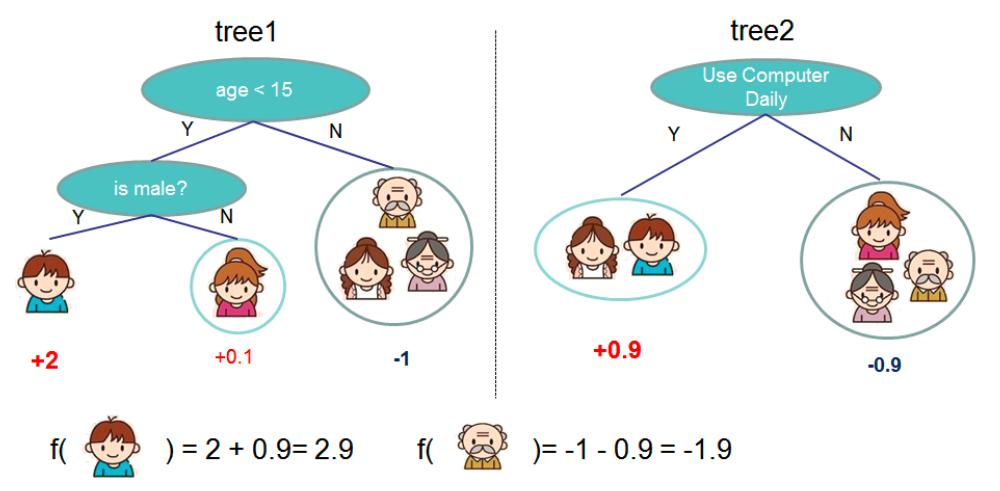
以决策树来作为基学习器来拟合梯度，即为GBDT。当前，GBDT及其变种（Xgboost、Light GBM、CatBoost）在各大算法比赛和工业界十分流行。

通过 GBDT 训练多个小的决策树往往要比一次性训练一个很大的决策树的效果好很多。多棵小树经过叠加后，比一棵大树要强。

tree_ensemble

2.1 GBDT的优势

GBDT的优势首先得益于决策树本身的一些良好特性，具体可以列举如下：

  • 决策树可以很好地处理missing feature
  • 决策树可以很好地处理各种类型的feature
  • 对异常样本（outlier）具有鲁棒性
  • 若特征集中存在不相关的feature，对模型的整体效果影响不大。

2.2 对 Gradient Boosting 的改进

使用 GBDT 时，我们可以使用一系列的正则化方法来防止过拟合，从而改善模型的泛化能力。

2.2.1 对树的约束

降低单棵树的模型复杂度，让每棵树为弱模型，这是改善整体模型泛化能力的关键。若单棵树的模型复杂度低，需要的树的数量就越多（迭代次数多大）。若单棵树的模型复杂度高，需要的树的数量就较少。

对树的生成的约束有：

  • 树的数量：树的数量越多，越容易导致过拟合。可使用早停（stop early）的方法，当观察到验证集的性能不再提升，即停止添加树。
  • 树的深度：深度越深，模型即越复杂。建议采用层次较浅的树。
  • 节点数量（叶子数量）：与树的深度类似，可用于调节树的大小（模型复杂度）。
  • 每次split的样本数：决策树采用贪心策略，依据信息增益等指标，对训练集进行划分（split），生成节点。限定每次split前的样本数，可调节树的模型复杂度。若当前的样本数小于指定的数量，则停止 split 。
  • 最小性能提升：对于每次split，限定split后，loss的减少量必须达到要求的阈值。否则，不进行split。
2.2.2 学习率

每棵树的预测结果会被相加，得到最后的预测结果。学习率（learning rate）衡量每棵树的贡献度（学习率 * 树的预测值）。学习率越低，通常迭代次数（树的数量）越大，泛化效果会更好一些。

2.2.3 随机梯度提升

训练每棵树时，仅使用整个训练集的其中一部分（随机采样），在加快训练速度的同时，可降低各基学习器的相关性，从而提高各基学习器的多样性。最后达到降低 boosting 的方差，提高泛化能力的效果。

随机提升有行采样和列采样两大类：

  • 对样本集进行随机采样（行采样，subsample rows）
  • 在创建树之前，对特征集进行随机采样（列采样，subsample columns）
  • 在每次split之前，对特征集进行随机采样（列采样，subsample columns）
2.2.4 正则化

对树的叶子节点的权重值使用正则化，如：l1正则化、l2正则化。

2.3 调参

GBDT 的参数调参可参考这个链接 。大致步骤依次如下：

  1. 选定一个相对较高的学习率（learning rate）。通常将学习率设定为 0.1。亦可视具体的情况，将学习率设置在 0.005 到 0.2 之间。
  2. 设定学习率后，根据模型在验证集的性能表现，选择最佳的树数量（迭代次数）。树的数量通常为 40 到 70 之间。适当的迭代次数，使得模型的训练时间较短，这有助于降低后面的步骤的调参的时间成本。
  3. 选择最佳的树参数（如树的深度、节点数等）：已设定的学习率和树数量后，根据模型在验证集的性能表现，选择最佳的单棵树的参数。
  4. 按比例地，降低学习率，增大树的数量，得到更健壮的模型。如，将学习率从 0.1 调整为 0.05，将树的数量从 60 调整为 120。

3、参考文献

  1. Friedman J H. Greedy function approximation: A gradient boosting machine.[J]. Annals of Statistics, 2001, 29(5): 1189-1232.
  2. Friedman J H. Stochastic Gradient Boosting
  3. Cheng Li. “A Gentle Introduction to Gradient Boosting”
  4. 维基百科：Gradient boosting
  5. Complete Guide to Parameter Tuning in Gradient Boosting (GBM) in Python
  6. A Gentle Introduction to the Gradient Boosting Algorithm for Machine Learning
  7. Introduction to Boosted Trees
  8. 周志华. 机器学习 [M]. 清华大学出版社, 2016.
  9. 李航. 统计学习方法[M]. 清华大学出版社, 2012.

版权声明：如需转载，请注明出处

Search

    Table of Contents